前言

昨天我們已經推導出貝爾曼方程，透過這個數學式，我們可以實現估計價值。在實務上，動態規劃適用迭代的方式，計算狀態或動作的價值。在書中提到有兩種迭代的方法，第一種是策略迭代(Policy iteration)，另一種是價值迭代(Value iteration)，這邊先介紹策略迭代方法。

策略迭代

先回頭看一下昨天推導出的狀態價值函數：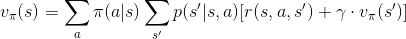

我們迭代的目標是狀態價值，而狀態的價值受到什麼影響呢？從符號上理解，狀態價值受策略 (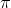) 影響。根據這個關係，數學家給出這樣的迭代規則：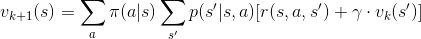

透過這條數學式，我們可以實現「根據現在的價值函數，估計新的價值函數。藉由重複獲得新的價值函數，我們可以逼近真實的狀態價值。」演算法如下：
(取自 Sutton 書籍)

這裡有兩件事值得注意：

1. 以策略為單位進行更新，也就是說我們經過一次迭代，所有的狀態價值都會更新，因此稱為策略迭代。
2. 演算法中雖然沒有特別說明，但所有新的價值函數，都是由舊的價值函數計算的，沒有先計算先更新的問題。(ex: 現在有狀態 A, B, C。更新 A 的價值後，若計算 B 時需要 A 的價值，仍使用舊的價值進行計算。)

範例：GridWorld

說了這麼多，還是比不上直接看程式運算的結果來的有說服力，這邊取用書上 Example 4.1 舉例。

想像現在有一個 4x4 大小的格子世界，最左上與最右下的格子是終點，如下圖灰色的部份：

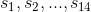• 狀態： ，表示處於的位置
• 動作：上、左、下、右
• 獎勵函數：都是 -1
• 其他規定：
  • 一次只能走一格
  • 撞牆回原位 (ex: 在位置 1 時，往上還是移動到位置 1)
  • 抵達終點後，不會離開終點

清點手邊的資訊，還缺轉移矩陣，根據其他規定我們可以自己實作，有興趣可以自己實作。
這邊提供我實作的 .npy 檔，是一個 16x16x4 的 numpy 陣列 (轉移後狀態 x 現在狀態 x 動作)

• 狀態：1~14 對應圖中格子的編號， 0 為左上的終點、 15 為右下的終點。
• 動作：上(0)、左(1)、下(2)、右(3)

明天我們將使用這些資訊，實作策略迭代評估狀態價值的過程。